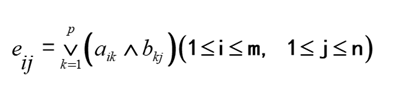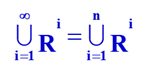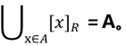离散数学定理与定义汇总

第一章：集合论

定义

• 定义1.1 (子集 Subset)：设A,B是任意两个集合，如果B中的每个元素都是A中的元素，则称B是A的子集合，简称子集，这时也称A包含B，或B被A包含，记作 A ⊇ B 或 B ⊆ A。
• 定义1.2 (真子集 Proper Subset)：设A,B是任意两个集合，如果 B ⊆ A 并且 A ≠ B，则称B是A的真子集，记作 B ⊂ A。
• 定义1.3 (空集 Empty Set)：不含任何元素的集合叫做空集，记作 ∅。
• 定义1.4 (全集 Universal Set)：在一个相对固定的范围内，包含此范围内所有元素的集合，称为全集或论集，用 U 或 E 表示。
• 定义1.5 (幂集 Power Set)：设A为任意集合，把A的所有不同子集构成的集合叫做A的幂集，记为 P(A) 或 2^A。其符号化表示为 P(A) = {x | 一切 x ⊆ A}。
• 定义1.6 (集合运算)：设U是全集，A，B是U的两个子集，则：
  • (1) 并集 (Union Set)：A ∪ B = {x | x ∈ A 或 x ∈ B}
  • (2) 交集 (Intersection Set)：A ∩ B = {x | x ∈ A 且 x ∈ B}
  • (3) 差集 (Difference Set)：A - B = {x | x ∈ A 且 x ∉ B}
  • (4) 补集 (Complement Set)：B^c = U - B = {x | x ∈ U 且 x ∉ B}
  • (5) 对称差集 (Symmetric Difference Set)：A ⊕ B = {x | (x ∈ A 且 x ∉ B) 或 (x ∈ B 且 x ∉ A)}
• 定义1.7 (等势 Equipotent)：设A，B是两个集合，若在A，B之间存在1-1对应关系 ψ：A → B，则称A与B等势，记为 A ~ B。
• 定义1.8 (可数集 Countable Set)：凡是与自然数集等势的集合，均称为可数集(可列集)。可数集的基数记为 א₀。
• 定义1.9 (不可数集 Uncountable Set)：称开区间(0,1)为不可数集，其基数记为 א；凡是与开区间(0,1)等势的集合都是不可数集。

定理

• 定理1.1 (外延性原理)：A = B 当且仅当A与B具有相同的元素，否则，A ≠ B。
• 定理1.2：设A、B是任意两个集合，则 A ⊆ B 且 B ⊆ A ⇔ A = B。
• 定理1.3：
  • (1) 空集是一切集合的子集。
  • (2) 空集是绝对唯一的。
• 定理1.4 (集合运算定律)：包括幂等律、交换律、结合律、分配律、同一律、零律、吸收律、双重否定律、德·摩根律、矛盾律、排中律。
• 定理1.5：
  • (1) 两个有限集等势当且仅当它们有相同的元素个数。
  • (2) 有限集不和其任何真子集等势。
  • (3) 可数集可以和其可数的真子集等势。

第二章：命题逻辑

定义

• 定义2.1 (命题 Proposition)：能够判断真假的陈述句称为命题。称“真”和“假”为命题的真值。
• 定义2.2 (否定式 Negation)：设P是任一命题，称复合命题“非P”(或“P的否定”)为P的否定式，记作 ¬P，称符号 ¬ 为否定联结词。
• 定义2.3 (合取 Conjunction)：设P、Q是任意两个命题，称复合命题“P并且Q”(或“P与Q”)为P与Q的合取，记作 P ∧ Q，称符号 ∧ 为合取联结词。
• 定义2.4 (析取 Disjunction)：设P、Q是任意两个命题，称复合命题“P或Q”为P与Q的析取，记作 P ∨ Q，称符号 ∨ 为析取联结词。
• 定义2.5 (蕴含式 Implication)：设P、Q是任意两个命题，称复合命题“如果P，则Q”为P与Q的蕴含式，记作 P → Q，称符号 → 为蕴含联结词，P为蕴涵式的前件，Q为蕴涵式的后件。
• 定义2.6 (等价 Equivalence)：设P、Q是任意两个命题，称复合命题“P当且仅当Q”为P与Q的等价，记作 P ↔ Q，称符号 ↔ 为等价联结词。
• 定义2.7 (命题公式 Propositional Formula / Well-formed Formula, WFF)：按规则生成的合式公式。
  • （1）命题变元G是命题公式；
  • （2）如果G是命题公式，则 (¬G) 也是命题公式；
  • （3）如果G，H是公式，则 (G ∧ H)、(G ∨ H)、(G → H)、(G ↔ H) 也是命题公式；
  • （4）有限次使用规则（1）、（2）和（3）后得到的符号串也是命题公式。
• 定义2.8 (解释 Instantiation / Assignment)：设P1、P2、…、Pn是出现在公式G中的所有命题变元，给P1、P2、…、Pn各指定一个真值，则称这些指定的真值组成G的一个解释(或赋值)，常记为Ｉ。
• 定义2.9 (公式类型)：在任意给定的解释I下，
  • 如果公式G的真值全为“真”，则称公式G为永真公式(或重言式) (Tautology)；
  • 如果公式G的真值全为“假”，则称公式G为永假公式(或矛盾式) (Contradiction)；
  • 如果公式G的真值至少存在一个为“真”，则称公式G为可满足公式 (Satisfiable Formula / Contingency)。
• 定义2.10 (逻辑等价 Equivalent)：设G，H是两个命题公式。如果对于所有解释，G与H的真值结果都相同，则称公式G与H是等价的，记为 G = H 或 G ⇔ H。
• 定义2.11 (联结词的完备集 Adequate set of Connectives)：
  • (1) 如果对任意一个命题公式，都可用S中的联结词进行等价表示，则称S是联结词的完备集。
  • (2) 设S是一个联结词的完备集且 T ⊂ S。如果至少存在一个命题公式不能用T中的联结词进行等价表示，则称S为极小联结词的完备集。
• 定义2.12 (文字 Literal)：称命题变元或命题变元的否定为文字。
• 定义2.13 (合取式/析取式)：
  • (1) 如果一个命题公式具有形式 A1 ∧ A2 ∧ … ∧ An (n≥1)，其中Ai是文字，则称该命题公式为合取式或短语 (Phrase)。
  • (2) 如果一个命题公式具有形式 A1 ∨ A2 ∨ … ∨ An (n≥1)，其中Ai是文字，则称该命题公式为析取式或子句 (Clause)。

注意：如果一个东西被括号括起来，说明它只能作为项，而不能认为是一个完整式子

e.g. 下列公式中，哪一个不是合取范式（D）
A. P and Q B. P or Q C. (P or Q) D. (P and Q)

其中C是合取范式的省略形式，不是析取范式

其中D 是析取范式的省略形式，不是合取范式

• 定义2.14 (合取范式/析取范式)：
  • (1) 如果一个命题公式具有形式 A1 ∧ A2 ∧ … ∧ An (n≥1)，其中Ai是析取式，则称该命题公式为合取范式 (Conjunctive Normal Form, CNF)。
  • (2) 如果一个命题公式具有形式 A1 ∨ A2 ∨ … ∨ An (n≥1)，其中Ai是合取式，则称该命题公式为析取范式 (Disjunctive Normal Form, DNF)。
• 定义2.15 (极小项/极大项)：在含有n个命题变元P1、P2、…、Pn的合取式(析取式)中，若每个命题变元与其否定不同时存在，但二者之一恰好出现一次且仅一次，则称此合取式为关于P1、P2、…、Pn的一个极小项 (Minterm) (析取式为极大项 (Maxterm))。
• 定义2.16 (主合取范式/主析取范式)：
  • (1) 如果一个命题公式具有形式 A1 ∧ A2 ∧ … ∧ An (n≥1)，其中Ai是极大项，则称该命题公式为主合取范式 (Principal Conjunctive Normal Form, PCNF)。
  • (2) 如果一个命题公式具有形式 A1 ∨ A2 ∨ … ∨ An (n≥1)，其中Ai是极小项，则称该命题公式为主析取范式 (Principal Disjunctive Normal Form, PDNF)。
• 定义2.17 (逻辑结果 Logic Conclusion)：设G1，G2，…，Gn，H是命题公式。对任意解释I，如果 G1 ∧ G2 ∧ … ∧ Gn 为真，H也为真，或者 G1 ∧ G2 ∧ … ∧ Gn 为假，则称H是G1，G2，…，Gn的逻辑结果，或者G1，G2，…，Gn共同蕴涵H，记为 G1，G2，…，Gn ⇒ H。
• 定义2.18 (有效推理 Valid Argument)：设G1，G2，…，Gn ，H是命题公式，如果H是G1，G2，…，Gn的逻辑结果，则称 G1，G2，…，Gn ⇒ H 为有效的或者正确的。
• 定义2.19 (消解 Resolution)：设G和H是两个析取式，如果G中有文字P，H中有文字 ¬P，则从G和H中分别消去P和 ¬P，并将G和H中余下的部分析取，构成一个新的析取式W，这个过程被称为消解，W称为G和H的消解式。

定理

• 定理2.1：公式G、H等价的充分必要条件是公式 G ↔ H 是永真公式。
• 定理2.2 (代入定理)：设G(P1,P2,…,Pn)是一个命题公式。若G是永真公式或永假公式，则用任意命题公式Gi分别取代Pi后得到的新命题公式G(G1,G2,…,Gn)也是一个永真公式或永假公式。
• 定理2.3 (替换定理)：设G1是G的子公式，H1是任意的命题公式。在G中凡出现G1处都用H1替换，得到新的命题公式H，若 G1 = H1，则 G = H。
• 定理2.4：对于任意命题公式，都存在与其等价的析取范式和合取范式。
• 定理2.5：任何一个公式都有与之等价的主析取范式和主合取范式。
• 定理2.6：公式H是前提集合Γ={G1,G2,…,Gn}的逻辑结果当且仅当 G1 ∧ G2 ∧ … ∧ Gn → H 为永真公式。
• 定理2.7 (消解原理)：如果W是G和H的消解式，则 G ∧ H ⇒ W。
• 4）I₆：┐G，G∨HÞH(选言三段论/Disjunctive Syllogism)
• 5）I₇：G，G→HÞH (分离规则/Modus Ponens)
• 6）I₈：┐H，G→HÞ┐G (否定后件式/Modus Tollens)
• 7）I₉：G→H，H→ＩÞG→Ｉ(假言三段论/Hypothelical Syllogism)
• 8）I₁₀：G∨H，G→Ｉ，H→ＩÞ(二难推论/Dilemma)

第三章：谓词逻辑

定义

• 定义3.1 (个体词/谓词)：在原子命题中，可以独立存在的客体称为个体词 (Individual)，用以刻画客体性质或客体之间关系的部分称为谓词 (Predicate)。
• 定义3.2 (n元谓词 Propositional Function)：设P(x1,x2,…,xn)是定义在Dn上的n元函数，其中D为非空的个体域。如果P(x1,x2,…,xn)的值域是{0，1}，则称P(x1,x2,…,xn)为n元命题函数或n元谓词。
• 定义3.3 (量词 Quantifier)：表达全部数量关系的词语如“一切”，“所有”，“每一个”等称为全称量词 (Universal Quantifier),记为 ∀。表达部分数量关系的词语如“存在”，“有一个”，“有一些”等称为存在量词 (Existential Quantifier)，记为 ∃。x被称为作用变量 (Function Variable)。量词的辖域是其后紧跟的谓词或公式。
• 定义3.4 (项 Term)：谓词逻辑中的项被递归地定义为：
  • （1）任意的常量符号或变量符号是项；
  • （2）若f(x1,x2,…,xn)是n元函数符号，t1，t2，…，tn是项，则f(t1,t2,…,tn)是项；
  • （3）有限次使用（1），（2）后得到的符号串也是项。
• 定义3.5 (原子谓词公式 Atomic Propositional Formulae)：若P(x1,x2,…,xn)是n元谓词，t1，t2，…，tn是项，则称P(t1,t2,…,tn)为原子谓词公式。
• 定义3.6 (合式谓词公式 Well-Formed Formulae/Wff)：
  • （1）原子公式是合式公式；
  • （2）若G，H是合式公式，则 (¬G)、(¬H)、(G ∨ H)、(G ∧ H)、(G → H) 和 (G ↔ H) 也是合式公式；
  • （3）若G是合式公式，x是个体变量，则 ∀xG、∃xG 也是合式公式；
  • （4）有限次使用（1）、（2）、（3）后得到的符号串也是合式公式。
• 定义3.7 (自由变元/约束变元)：给定公式 ∀xG 和 ∃xG，G为 ∀x 和 ∃x 的辖域，则G中x的出现都是约束出现 (Bound Occurrence)，称变元x为约束变元 (Bound Variable)，G中的不同于x的其他变元的出现则是自由出现 (Free Occurrence)，称这些变元为自由变元 (Free Variable)。
• 定义3.8 (封闭公式 Closed Formula)：设G是任意一个公式，若G中无自由变元，则称G为封闭的公式，简称闭式。
• 定义3.9 (谓词公式的解释 Interpretation)：谓词逻辑中谓词公式G的每一个解释I由如下四部分组成：
  • （1）非空的个体域D；
  • （2）G中的每个常量符号，指定D中的某个特定元素；
  • （3）G中的每个n元函数符号，指定Dn到D的某个特定函数；
  • （4）G中的每个n元谓词符号，指定Dn到｛0,1｝的某个特定谓词。
• 定义3.10 (谓词公式类型)：在任意给定的解释I下，如果谓词公式G的取值全为“真”，则称G为永真公式 (Tautology)；如果谓词公式G的取值全为“假”，则称G为永假公式 (Contradiction)；如果G的取值至少存在一个为“真”，则称谓词公式Ｇ为可满足公式 (Contingency)。
• 定义3.11 (谓词逻辑等价 Equivalent)：设G，H是谓词公式，如果谓词公式 G ↔ H 是永真公式，那么称G，H是等价的，记为 G = H 或 G ⇔ H。
• 定义3.12 (代入实例 Substitution Instance)：设G(P1,P2,…,Pn)是命题公式，P1,P2,…,Pn是出现在G中的命题变元，当用任意的谓词公式Gi取代Pi(i=1,2,…,n)，得到新的谓词公式G′(G1,G2,…,Gn)，则称G′(G1,G2,…,Gn)为G(P1,P2,…,Pn)的代入实例。
• 定义3.13 (前束范式 Prenex Normal Form)：具有形式 Q1x1 Q2x2…QnxnM(x1,x2,…,xn) 的谓词公式，其中Qi为量词 ∀ 或 ∃，M(x1,x2,…,xn)为不含量词的公式。
• 定义3.14 (Skolem范式 Skolem Normal Form)：在前束合取范式的基础上，通过特定规则消除存在量词得到的范式。
• 定义3.15 (对y自由)：在谓词公式G(x)中，若x不自由出现在量词 ∀y 或者 ∃y 的辖域中，则称G(x)对于y是自由的。

定理

• 定理3.1：永真公式的任意一个代入实例必为永真公式。
• 定理3.2 (前束范式存在性定理)：谓词逻辑中的任一谓词公式都可化为与之等价的前束范式，但其前束范式并不唯一。

第四章：二元关系

定义

• 定义4.1 (序偶 Ordered Couple/Pair)：由两个元素x，y按照一定的次序组成的二元组被称为有序偶对，简称序偶，记作 <x,y>。
• 定义4.2 (序偶相等)：给定序偶 <a,b> 和 <c,d>，<a,b> = <c,d> ⇔ a=c 且 b=d。
• 定义4.3 (笛卡尔积 Cartesian Product)：设A，B是两个集合，称集合 A × B = {<x,y> | x ∈ A ∧ y ∈ B} 为集合A与B的笛卡尔积。
• 定义4.4 (n元笛卡尔积)：设A1,A2,…,An是n个集合，称 A1 × A2 × … × An = {<a1,a2,…,an> | (ai ∈ Ai) ∧ i ∈ {1,2,3,…,n}} 为集合A1,A2,…,An的笛卡尔积。
• 定义4.5 (二元关系 Binary Relation)：设A,B为两个非空集合，称 A × B 的任何子集R为从A到B的二元关系，简称关系，记作 R：A → B；如A＝B，则称R为A上的二元关系。
• 定义4.6 (n元关系 n-ary Relation)：设A1，A2，…，An为n个非空集合，则称 A1 × A2 × … × An 的子集R为以A1 × A2 × … × An为基的n元关系。
• 定义4.7 (布尔矩阵运算)：
  • (1) 布尔并 (Boolean Join)：A ∨ B = C = (cij)，其中 cij = aij ∨ bij。
  • (2) 布尔交 (Boolean Meet)：A ∧ B = D = (dij)，其中 dij = aij ∧ bij。
  • (3) 布尔积 (Boolean Product)：A ⊙ B = E = (eij)，其中

    

    。
• 定义4.8 (复合关系 Composite Relation)：设A,B,C是三个集合，R：A → B，S：B → C，则R与S的复合关系是从A到C的关系，记为 R ∘ S，其中 R ∘ S = {<x,z> | x ∈ A ∧ z ∈ C ∧ ∃y(y ∈ B ∧ <x,y> ∈ R ∧ <y,z> ∈ S)}。
• 定义4.9 (逆关系 Inverse Relation)：设A，B是两个集合， R：A → B ，则从B到A的关系 R^(-1) = {<b,a> | <a,b> ∈ R} 称为R的逆关系。
• 定义4.10 (关系的幂 Powers of a Relation)：设 R：A → A ，则R的n次幂，记为Rn，定义如下：
  • (1) R⁰ = IA = {<a,a> | a ∈ A}；
  • (2) R¹ = R；
  • (3) Rⁿ⁺¹ = Rⁿ ∘ R = R ∘ Rⁿ。
• 定义4.11 (自反性/反自反性)：设R是非空集合A上的关系，
  • (1) 如果 ∀x(x ∈ A → <x,x> ∈ R) = 1，那么称R在A上是自反的 (Reflexive)。
  • (2) 如果 ∀x(x ∈ A → <x,x> ∉ R) = 1，那么称R在A上是反自反的 (Irreflexive/Anti-reflexive)。
• 定义4.12 (对称性/反对称性)：设R是非空集合A上的关系。
  • (1) 如果 ∀x∀y(x ∈ A ∧ y ∈ A ∧ <x,y> ∈ R → <y,x> ∈ R) = 1，则称关系R是对称的 (Symmetric)。
  • (2) 如果 ∀x∀y(x ∈ A ∧ y ∈ A ∧ (<x,y> ∈ R ∧ <y,x> ∈ R) → x=y) = 1，则称关系R是反对称的 (Antisymmetric)。
• 定义4.13 (传递性 Transitivity)：设R是非空集合A上的关系。如果 ∀x∀y∀z(x ∈ A ∧ y ∈ A ∧ z ∈ A ∧ <x,y> ∈ R ∧ <y,z> ∈ R → <x,z> ∈ R) = 1，则称关系R是传递的 (Transitive)。
• 定义4.14 (关系的闭包 Closure)：设R是定义在A上的关系，若存在A上的另一个关系R′使得 R ⊆ R′ 且满足：
  • （1）R′是自反的(对称的、或传递的)；
  • （2）对任何自反的(对称的、或传递的)关系R〞，如果 R ⊆ R〞，就有 R′ ⊆ R〞。
  • 则称R′为R的自反闭包 (Reflexive Closure) (记为 r(R))、对称闭包 (Symmetric Closure) (记为 s(R))、或传递闭包 (Transitive Closure) (记为 t(R))。

定理

• 定理4.1：设A,B,C是任意三个集合，则笛卡尔积对并集和交集满足分配律。

  • (1) A × (B ∪ C) = (A × B) ∪ (A × C)
  • (3) A × (B ∩ C) = (A × B) ∩ (A × C) (左右分配均成立)

• 定理4.2：设A,B,C,D是任意四个非空集合，则 A × B ⊆ C × D ⇔ A ⊆ C 且 B ⊆ D。

• 定理4.3：布尔矩阵的并和交运算满足交换律、结合律；布尔积满足结合律；布尔交对布尔并满足分配律，布尔并对布尔交满足分配律。

• 定理4.4：设A、B、C和D是任意四个集合，R:A→B，S:B→C，T:C→D，则

  • （1）(R ∘ S) ∘ T = R ∘ (S ∘ T) (复合运算的结合律)；
  • （2）I_A ∘ R = R ∘ I_B = R。

• 定理4.5：关系的复合运算对并运算满足分配律，对交运算只满足包含关系。

  • （1）R ∘ (S₁ ∪ S₂) = (R ∘ S₁) ∪ (R ∘ S₂)；
  • （3）R ∘ (S₁ ∩ S₂) ⊆ (R ∘ S₁) ∩ (R ∘ S₂)。

• 定理4.6：设R,S分别是从A到B，B到C的二元关系，则 (R ∘ S)^-1 = S^-1 ∘ R^-1。

• 定理4.7：设 R：A→B，S：A→B，则逆运算对并、交、差运算满足分配性，逆运算与补运算可交换，逆运算保持包含关系。

• 定理4.8：设A是有限集合，且 |A| = n，R是A上的关系，则

  

• 定理4.9：设R是集合A上的二元关系，则：

  • （1）R是自反的 ⇔ I_A ⊆ R；
  • （2）R是反自反的 ⇔ R ∩ I_A = ∅；
  • （3）R是对称的 ⇔ R = R^-1；
  • （4）R是反对称的 ⇔ R ∩ R^-1 ⊆ I_A；
  • （5）R是传递的 ⇔ R ∘ R ⊆ R。

• 定理4.10 (关系性质的保守性，部分)：

  • (1) 若R,S是自反的，则 R^-1, R ∪ S, R ∩ S, R ∘ S 也是自反的。
  • (3) 若R,S是对称的，则 R^-1, R ∪ S, R ∩ S 也是对称的。
  • (5) 若R,S是传递的，则 R^-1, R ∩ S 也是传递的。

• 定理4.10 (闭包的计算公式)：设R是集合A上的二元关系，则：

  • （1）r(R) = R ∪ IA。
  • （2）s(R) = R ∪ R^-1。
  • （3）t(R) = R ∪ R² ∪ R³ ∪ … (若 |A| = n，则 t(R) = R ∪ R² ∪ … ∪ Rⁿ)。

第五章：特殊关系

定义

• 定义5.1 (相容关系 Compatibility Relation)：设R是定义在非空集合A上的关系，如果R是自反的、对称的，则称R是A上的相容关系。
• 定义5.2 (覆盖 Covering)：给定非空集合A，设有集合S＝{A1,A2,…,Am}。如果 (1) Ai ⊆ A 且 Ai ≠ ∅， i=1，2，…，m ； (2) ∪ Ai = A。则S被称作集合A的一个覆盖。
• 定义5.3 (等价关系 Equivalence Relation)：设R是定义在非空集合A上的关系，如果R是自反的、对称的、传递的，则称R为A上的等价关系。
• 定义5.4 (划分 Partition)：给定非空集合A，设有集合S={A1,A2,…,Am}。如果满足 (1) Ai ⊆ A 且 Ai ≠ ∅； (2) Ai ∩ Aj = ∅，i ≠ j； (3) ∪ Ai = A。则称S为集合A的一个划分，Ai叫做这个划分的块(Block)或类(Class)。
• 定义5.5 (等价类 Equivalence Class)：设R是非空集合A上的等价关系，对 ∀x ∈ A，称集合 [x]R = {y | y ∈ A ∧ <x,y> ∈ R} 为x关于R的等价类。
• 定义5.6 (商集 Quotient Set)：设R是非空集合A上的等价关系，由R确定的一切等价类构成的集合，称为集合A上关于R的商集，记为 A/R = {[x]R | x ∈ A}。
• 定义5.7 (拟序关系 Quasi-Order Relation)：设R是非空集合A上的关系，如果R是反自反的、反对称的和传递的，则称R是A上的拟序关系，简称拟序，记为 <。序偶 <A,< 称为拟序集。
• 定义5.8 (拟序关系-简化)：设R是非空集合A上的关系，如果R是反自反和传递的，则称R是A上的拟序关系 (PPT中此定义与5.7略有出入，5.7更标准)。
• 定义5.9 (偏序关系 Partial Order Relation)：设R是非空集合A上的关系，如果R是自反的、反对称的和传递的，则称R是A上的偏序关系，简称偏序，记为 ≤。序偶 <A,≤> 称为偏序集 (Poset)。
• 定义5.10 (最大元/最小元 Greatest/Smallest Element)：设 <A,≤> 是偏序集，B是A的非空子集。
  • （1）如果 ∃b(b ∈ B ∧ ∀x(x ∈ B → x ≤ b)) = 1，则称b为B的最大元素。
  • （2）如果 ∃b(b ∈ B ∧ ∀x(x ∈ B → b ≤ x)) = 1，则称b为B的最小元素。
• 定义5.11 (极大元/极小元 Maximal/Minimal Element)：设 <A,≤> 是偏序集，B是A的非空子集。
  • （1）如果 ∃b(b ∈ B ∧ ∀x(x ∈ B ∧ b ≤ x → x = b)) = 1，则称b为B的极大元素。
  • （2）如果 ∃b(b ∈ B ∧ ∀x(x ∈ B ∧ x ≤ b → x = b)) = 1，则称b为B的极小元素。
• 定义5.12 (上界/下界/上确界/下确界)：设 <A,≤> 是偏序集，B是A的任何一个子集。
  • （1）如果 ∃a(a ∈ A ∧ ∀x(x ∈ B → x ≤ a)) = 1，则称a为B的上界 (Upper Bound)。
  • （2）如果 ∃a(a ∈ A ∧ ∀x(x ∈ B → a ≤ x)) = 1，则称a为B的下界 (Lower Bound)。
  • （3）令C={y|y是B的上界}，则称C的最小元为B的最小上界 (Least Upper Bound, LUB) 或 上确界 (Supremum, supB)。
  • （4）令D={y|y是B的下界}，则称D的最大元为B的最大下界 (Greatest Lower Bound, GLB) 或 下确界 (Infimum, infB)。
• 定义5.13 (全序关系 Total Order Relation)：设 <A,≤> 是一个偏序关系，若对 ∀x ∈ A，∀y ∈ A，总有 x ≤ y 或 y ≤ x 之一成立，则称关系 ≤ 为全序关系。<A,≤> 称为全序集或链 (Chain)。
• 定义5.14 (良序关系 Well-Order Relation)：设 <A,≤> 是一偏序集，若A的任何一个非空子集都有最小元，则称 ≤ 为良序关系。<A,≤> 称为良序集。
• 定义5.15 (函数 Function/Mapping)：设f是集合A到B的关系，如果对每个 x ∈ A，都存在惟一的 y ∈ B，使得 <x,y> ∈ f，则称关系f为A到B的函数，记为 f: A → B。
• 定义5.16 (函数类型)：设f是从集合A到集合B的函数。
  • （1）单射 (Injection)：∀x1,x2 ∈ A (x1 ≠ x2 → f(x1) ≠ f(x2))。
  • （2）满射 (Surjection)：ran f = B。
  • （3）双射 (Bijection)：既是单射，又是满射。
  • （4）变换 (Transformation)：A上的双射函数。
• 定义5.17 (一些重要函数)：恒等函数、常值函数、特征函数、上取整函数、下取整函数、布尔函数。
• 定义5.18 (特定数学函数)：Sigmoid函数, tanh函数, ReLU函数。
• 定义5.19 (复合函数 Composition Function)：设 f：A → B，g：B → C 是两个函数，如果f与g的复合关系 f ∘ g = {<x,z> | x ∈ A ∧ z ∈ C ∧ ∃y(<x,y> ∈ f ∧ <y,z> ∈ g)} 是从A到C的函数，则称 f ∘ g 为f与g的复合函数 (注意PPT中记号为 f ∘ g 但计算为 g(f(x))，通常标准记号 g ∘ f 表示 g(f(x)))。
• 定义5.20 (逆函数 Inverse Function)：设 f: A → B 的函数。如果 f^(-1) = {<y,x> | x ∈ A ∧ y ∈ B ∧ <x,y> ∈ f} 是从B到A的函数，则称 f^(-1)：B → A 是函数f的逆函数。
• 定义5.21 (置换 Permutation)：设A是有限集合。从A到A的双射函数称为A上的置换或排列。

定理

• 定理5.1：给定集合A的一个覆盖S＝{A1,A2,…,An} ，设 R = A1×A1 ∪ A2×A2 ∪ … ∪ An×An，则R是A上的相容关系。
• 定理5.2 (等价类的性质)：设R是非空集合A上的等价关系，则：
  • (1) 对 ∀x ∈ A，[x]R ≠ ∅。
  • (2) 对 ∀x ∈ A, ∀y ∈ A，a) 如果 y ∈ [x]R，则有 [x]R = [y]R， b) 如果 y ∉ [x]R，则有 [x]R ∩ [y]R = ∅。
  • (3)

    

• 定理5.3：设R是非空集合A上的等价关系，则A对R的商集A/R是A的一个划分，称之为由R所导出的等价划分。
• 定理5.4：给定集合A的一个划分Π={A1,A2,…,An}， 则由该划分确定的关系 R=(A1×A1)∪(A2×A2)∪…∪(An×An) 是A上的等价关系。
• 定理5.5 (特殊元素关系)：
  • （1）b是B的最大元 ⇒ b是B的极大元、上界、上确界；
  • （2）b是B的最小元 ⇒ b是B的极小元、下界、下确界；
  • （3）a是B的上确界，且a∈B ⇒ a是B的最大元；
  • （4）a是B的下确界，且a∈B ⇒ a是B的最小元。
• 定理5.6 (特殊元素唯一性等)：
  • （1）若B存在最大元，则B的最大元是惟一的；
  • （3） b是B的最大元 ⇔ b是B的惟一极大元；
  • （5）若B存在上确界，则B的上确界是惟一的。 (最小元、极小元、下确界类似)
• 定理5.7：设A，B是有限集合，且 |A|=|B|，f是A到B的函数，则f是单射当且仅当f是满射。
• 定理5.8 (复合函数的性质)：设f和g分别是A到B和从B到C的函数，则：
  • (1) 如f,g是满射，则 g ∘ f 也是从A到C满射；
  • (2) 如f,g是单射，则 g ∘ f 也是从A到C单射；
  • (3) 如f,g是双射，则 g ∘ f 也是从A到C双射。
• 定理5.9 (复合函数反推性质)：设f和g分别是A到B和B到C的函数，则
  • （1）如 g ∘ f 是A到C的满射，则g是B到C 的满射；
  • （2）如 g ∘ f 是A到C的单射，则f是A到B的单射。
• 定理5.10 (逆函数的性质)：设f是A到B的双射函数，则： f^-1 ∘ f = I_A； f ∘ f^-1 = I_B。
• 定理5.11：若f是A到B的双射，则f的逆函数 f^-1 也是B到A的双射。

第六章：图论基础

定义

• 定义6.1 (图 Graph)：一个图是一个序偶 <V, E>，其中V是有限非空结点集，E是有限边集。
• 定义6.2 (邻接矩阵 Adjacency Matrix)：设图 G = <V, E>，V = {v1, …, vn}，则n阶方阵 AG = (aij) 称为G的邻接矩阵，其中 aij 表示从vi到vj的边数（简单图中为1或0）。
• 定义6.3 (图的操作)：删除边、删除结点、边收缩、加新边。
• 定义6.4 (邻接点/邻接边/环/孤立点等)：
  • 邻接点 (Adjacent Point)：边e的两个端点。
  • 邻接边 (Adjacent Edge)：具有公共结点的两条边。
  • 环 (Loop/Self-Loop)：两个端点相同的边。
  • 孤立结点 (Isolated Point)：不与任何结点相邻接的结点。
• 定义6.5 (图的分类-按边方向)：无向图、有向图、混合图。
• 定义6.6 (图的分类-按平行边)：
  • 平行边 (Parallel Edge)：连接相同端点（有向图还需方向相同）的多条边。
  • 多重图 (Multigraph)：含有平行边的图。
  • 线图 (Line Graph)：非多重图。
  • 简单图 (Simple Graph)：无环的线图。
• 定义6.7 (赋权图 Weighted Graph)：边或结点关联一个数值（权）。
• 定义6.8 (子图 Subgraph)：设图 G = <V, E> 和图 G1 = <V1, E1>。若 V1 ⊆ V，E1 ⊆ E，则称G1是G的子图。
  • 生成子图 (Spanning Subgraph)：V1 = V。
  • 导出子图 (Induced Subgraph)：由V的子集V2导出的子图，包含V2中所有结点及它们之间在G中的所有边。
• 定义6.9 (完全图 Complete Graph)：Kn是n个结点的无向简单图，任意两结点间都有边。
• 定义6.10 (补图 Complement of Graph)：对于简单图G，G^c = <V, E_Kn - E_G>。
• 定义6.11 (结点的度 Degree)：
  • (无向图) deg(v)：以结点v为端点的边数 (环计两次)。
  • (有向图) deg+(v) (出度), deg-(v) (入度)。
• 定义6.12 (度数序列 Degree Sequence)：图G的结点集V = {v1, …, vn}的度数序列为 (deg(v1), …, deg(vn))。
• 定义6.13 (图的同构 Isomorphism)：图G与G’同构，若存在结点间的双射g，保持边的邻接关系和重数。
• 定义6.14 (通路/回路 Walk/Circuit)：
  • 通路 (Walk)：结点和边相继交错出现的序列 v0e1v1…ekvk。长度为k。
  • 回路 (Circuit/Closed Walk)：始点和终点相同的通路。
  • 简单通路 (Simple Walk/Trail)：所有边互不相同。
  • 基本通路 (Elementary Path/Path)：所有结点互不相同。
  • 基本回路 (Elementary Circuit/Cycle)：除首尾外所有结点互不相同。
• 定义6.15 (可达/距离 Reachable/Distance)：
  • 可达的 (Reachable)：若vi到vj存在通路。
  • 距离 (Distance) d(vi, vj)：vi到vj的短程线 (Geodesic) 的长度。
• 定义6.16 (可达性矩阵 Accessibility Matrix)：P = (pij)，若vi到vj可达则pij=1，否则为0。
• 定义6.17 (连通图/非连通图 Connected/Disconnected Graph - 无向图)：若无向图G中的任何两个结点都是可达的，则称G是连通图。
• 定义6.18 (连通分支 Connected Component - 无向图)：无向图G中结点之间的可达关系R的每个等价类导出的子图。
• 定义6.19 (有向图的连通性)：
  • 弱连通图 (Weakly Connected Graph)：其基础无向图连通。
  • 单向连通图 (Unilaterally Connected Graph)：任两结点u,v，u到v可达或v到u可达。
  • 强连通图 (Strongly Connected Graph)：任两结点u,v，u到v可达且v到u可达。
• 定义6.20 (强/单向/弱连通分支 - 有向图)：图G的极大强/单向/弱连通子图。

定理

• 定理6.1 (握手定理 Handshaking Theorem)：图中结点度数的总和等于边数的二倍。
  • 推论6.1：图中度数为奇数的结点个数为偶数。
• 定理6.2 (有向图度定理)：有向图中各结点的出度之和等于各结点的入度之和，等于边数。
• 定理6.3：设A为图G的邻接矩阵，Am为A的m次幂。则Am中的元素 a_ij^(m) 为从结点vi到结点vj长度为m的通路数目。
• 定理6.4：在一个具有n个结点的图中，如果从结点vi到结点vj（vi ≠ vj）存在一条通路，则从vi到vj存在一条长度不大于n-1的通路。
• 定理6.5：在一个具有n个结点的图中，如果存在经过结点vi回路，则存在一条经过vi的长度不大于n的回路。
• 定理6.6：利用 Bn-1 = I + A + … + A^(n-1) 判断可达性及计算距离。
• 定理6.7：可达性矩阵 P = I ∨ A ∨ A(2) ∨ … ∨ A(n-1) (布尔运算)。
• 定理6.8：无向图G中结点之间的可达关系是等价关系。
• 定理6.9：有向图G是强连通图的充分必要条件是G中存在一条经过所有结点的回路。
• 定理6.10：有向图G是单向连通图的充分必要条件是G中存在一条经过所有结点的通路。
• 定理6.11：在有向图G中，它的每一个结点位于且仅位于一个强（弱）连通分支中。
• 定理6.12：在有向图G中，它的每一个结点至少位于一个单向连通分支中。
• 定理6.13：在有向图G中，它的每一条边至多在一个强连通分支中；至少在一个单向连通分支中；在且仅在一个弱连通分支中。

第七章：特殊图

定义

• 定义7.1 (无向树 Undirected Tree)：连通而不含回路的无向图称为无向树。
  • 叶 (Leaf)：度数为1的结点。
  • 分支点 (Branch Point) / 内部结点 (Internal Node)：度数大于1的结点。
  • 森林 (Forest)：每个连通分支都是树的无向图。
• 定义7.2 (生成树 Spanning Tree)：给定图G，若G的某个生成子图是树，则称之为G的生成树。
• 定义7.3 (最小生成树 Minimal Spanning Tree)：设G是连通的赋权图，T是G的一棵生成树，T的每个树枝所赋权值之和称为T的权。G中具有最小权的生成树称为G的最小生成树。
• 定义7.4 (有向树 Directed Tree)：一个有向图，若略去所有有向边的方向所得到的无向图是一棵树，则这个有向图称为有向树。
• 定义7.5 (根树 Rooted Tree)：一棵非平凡的有向树，如果恰有一个结点的入度为0（称为根 Root），其余所有结点的入度均为1。
  • 叶 (Leaf)：出度为0的结点。
  • 内点 (Internal Point)：入度为1，出度大于0的结点。
  • 分支点 (Branch Point)：内点和根。
  • 层数 (Level Number)：从根到任一结点v的通路长度。
  • 高 (Height)：所有结点的层数中最大的。
• 定义7.6 (家族关系 - 根树)：祖先、后代、父亲、儿子、兄弟。
• 定义7.7 (有序树 Ordered Tree)：在根树中规定了每一层上结点的次序的根树。
• 定义7.8 (k元树 k-ary Tree)：
  • 注意，此处定义与广泛接收的定义有区别（翻译不同）
  • (1) 若T的每个分支点至多有k个儿子，则称T为k元树。
  • (2) 若T的每个分支点都恰有k个儿子，则称T为完全k元树 (Complete k-ary Tree)。
  • (3) 若T是k元完全树且每个叶结点的层数均为树高，则称T为满k元树 (Full k-ary Tree)。
• 定义7.9 (前缀码 Prefixed Code)：设A是一个符号串集合，若对任意 bi, bj ∈ A，bi ≠ bj，bi不是bj的前缀，bj也不是bi的前缀，则称A为前缀码。
• 定义7.10 (最优树 Optimal Tree)：赋权二元树中，带权路径长度 (∑ wi * L(wi)) 最小的树。
• 定义7.11 (欧拉通路/回路 Eulerian Path/Circuit)：经过图中每边一次且仅一次的通路(回路)。
• 定义7.12 (欧拉图 Eulerian Graph)：具有欧拉回路的图。
• 定义7.13 (桥 Bridge / Cut edge)：设G = <V, E>，e∈E，如果 p(G-e) > p(G) (p为连通分量数)，称e为G的桥。
• 定义7.14 (哈密顿通路/回路 Hamiltonian Path/Circuit)：经过图中每个结点一次且仅一次的通路（回路）。
• 定义7.15 (哈密顿图 Hamiltonian Graph)：存在哈密顿回路的图。
• 定义7.16 (偶图 Bipartite Graph)：若无向图G的结点集V能够划分为两个子集V1, V2 (V1∩V2=∅, V1∪V2=V)，使得G中任意一条边的两个端点，一个属于V1，另一个属于V2。
• 定义7.17 (完全偶图 Complete Bipartite Graph)：在偶图G = <V1, E, V2>中，若V1中的每个结点与V2中的每个结点都有且仅有一条边相关联，记为 Ki,j。
• 定义7.18 (匹配 Matching)：在偶图G = <V1, E, V2>中，从V1到V2的一个完全匹配是E的子集E’，使得V1中每个结点都是E’中某条边的端点，且E’中任意两条边没有公共端点。
• 定义7.19 (平面图 Planar Graph)：如果能把一个无向图G的所有结点和边画在平面上，使得任何两边除公共结点外没有其他交叉点。
• 定义7.20 (面 Face/Region)：在平面图G的一个平面表示中，由边所包围的其内部不包含图的结点和边的区域。
  • 面的次数 (Degree of a face) D(r)：包围该面的边界的长度。

定理

• 定理7.1 (树的等价性质)：
  • G连通而不含回路 (即G是树)
  • G中无回路，且 m = n-1
  • G是连通的，且 m = n-1
  • G中无回路，但在G中任二结点之间增加一条新边，就得到惟一的一条基本回路
  • G是连通的，但删除G中任一条边后，便不连通 (n≥2)
  • G中每一对结点之间有惟一一条基本通路 (n≥2)
• 定理7.2：任意非平凡树T都至少有两片叶。
• 定理7.3：一个图G存在生成树T_G的充分必要条件是G是连通的。
• 定理7.4：在k元完全树中，若叶数为t，分支点数为i，则有 (k-1) × i = t-1。
• 定理7.5 (无向图欧拉通路/回路判定)：无向图G具有一条欧拉通路，当且仅当G是连通的，且仅有零个或两个奇度数结点。
  • 推论7.1：无向图G具有欧拉回路，当且仅当G是连通的，并且所有结点的度数均为偶数。
• 定理7.6 (有向图欧拉通路判定)：有向图G具有欧拉通路，当且仅当G是连通的，且除了两个结点以外，其余结点的入度等于出度，而这两个例外的结点中，一个结点的入度比出度大1，另一个结点的出度比入度大1。
  • 推论7.2：有向图G具有欧拉回路，当且仅当G是连通的，且所有结点的入度等于出度。
• 定理7.7 (哈密顿图必要条件)：设无向图G是哈密顿图，V1是V的任意非空子集，则 p(G-V1) ≤ |V1|。
  • 推论7.3：设无向图G中存在哈密顿通路，则对V的任意非空子集V1，都有 p(G-V1) ≤ |V1| + 1。
• 定理7.8 (哈密顿通路充分条件 - Ore类型)：设G是具有n个结点的简单无向图。如果对任意两个不相邻的结点u, v∈V，均有 deg(u) + deg(v) ≥ n - 1，则G中存在哈密顿通路。
  • 推论7.4 (哈密顿回路充分条件 - Ore定理)：如果对任意两个不相邻的结点u, v∈V，均有 deg(u) + deg(v) ≥ n，则G中存在哈密顿回路。
  • 推论7.5 (哈密顿回路充分条件 - Dirac定理)：如果对任意v∈V，均有 deg(v) ≥ n/2 (n≥3)，则G是哈密顿图。
• 定理7.9：设G是有n (n ≥ 2)个结点的一些简单有向图。如果忽略G中边的方向所得的无向图中含生成子图Kn，则有向图G中存在哈密顿通路。
• 定理7.10 (偶图判定)：无向图G为偶图的充分必要条件是G的所有回路的长度均为偶数（即不含奇圈）。
• 定理7.11 (霍尔(Hall)定理/婚姻定理)：偶图G = <V1, E, V2>中存在从V1到V2的匹配的充分必要条件是V1中任意k个结点至少与V2中的k个结点相邻，k = 1, 2, …, |V1|。
• 定理7.12 (匹配的t条件)：设G = <V1,E,V2>是一个偶图。如果满足条件（1）V1中每个结点至少关联t条边；（2）V2中每个结点至多关联t条边；则G中存在从V1到V2的匹配。
• 定理7.13 (平面图面度数和)：平面图中所有面的次数之和等于边数的二倍。
• 定理7.14 (欧拉公式 Euler’s Formula)：设G是连通平面图，若它有n个结点、m条边和r个面，则有 n – m + r = 2。
  • 推论7.6：设G是一个(n, m)简单连通平面图，若m＞1，则有 m ≤ 3n – 6。
  • 推论7.7：设G是一个(n, m)简单连通平面图，若每个面的次数至少为k (k ≥ 3)，则有 (k - 2)m ≤ k(n - 2)。
• 定理7.15 (库拉托夫斯基定理 Kuratowski’s Theorem)：一个图是平面图的充分必要条件是它的任何子图都不可能收缩（或同胚）为K5或K3,3。